This class is an introduction to computer graphics in two and three-dimensions. In this class we learn how these images are made, and in particular, how graphics libraries and programs work. This class is not about using existing programs to create animation and images -- rather it is about how such programs work. That said, we will generate some interesting stills and animations, and have fun doing it!

Creating realistic renderings of three-dimensional scenes is quite complicated (spatial coordinates, lighting calculations, etc.) and we will examine several different approaches to generating these images. Our main focus will be on using OpenGL, an industry standard three-dimensional graphics library with a high degree of platform independence.

The approach taken in the course will be to get into the three-dimensional graphics as soon as possible so that there will be time during the semester to work on interesting and challenging programming projects. Then, during the last third of the semester, we will backtrack and use class time to explore how graphics implementations work, including the underlying mathematics.

The programming projects themselves will build upon each other in a natural way. We will first examine some simple shapes in two-dimensions, then program in user interaction and animation. Then we will expand these shapes into three-dimensions and discuss the lighting and and materials properties that determine how realistic the rendering appears. Finally we will put it all together in an interactive three-dimensional program that will let us explore our shapes "up-close and personal".

Below are sample images from some of the projects that have been worked on in this course in the past. While we may not do projects involving these particular figures, these serve to provide an idea of the type of work that we will be done.

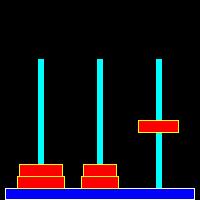
The Towers of Hanoi

	A classic example in computer science lore is the Towers of Hanoi puzzle, often used as an example of a problem that lends itself to a recursive solution. The solution of this puzzle makes a very nice animation.
	Once the concept of animation are understood, one can combine this with efforts to create three-dimensional scenes. This is a frame from a animation showing the solution of the Towers of Hanoi puzzle in three-dimensions. Notice the reflection of the disks on the base.

Sierpinski Gasket

Here is an approximation of the three-dimensional version of the Sierpinski Gasket. It is constructed recursively by staring with a solid tetrahedron specified by it's four vertices. The next step is to find the midpoints of each edge and remove the tetrahedron that has these four points as it's vertices. The result of this operations is four tetrahedra, three acting as a base and one resting on top of the other three. This process is repeated to a specified depth of recursion on each of the tetrahedra that results at each step.

Menger Sponge

This is an approximation of the Menger Sponge. Like the Sierpinski Gasket it is constructed recursively. However, to get this figure one starts with a single cube. Then, divide it into 27 equal cubes so that there are nine smaller cubes on each face of the original cube. Now remove the middle small cube from each face and the one in the center of the large cube, leaving 20 small cubes. Finally, repeat the procedure on each of the smaller cubes, continuing in this fashion until some specified depth of recursion is reached.