NTIC Improving the PNT

Section 25.2 Improving the PNT

We can build an interactive table of some results if we are online.

xxxxxxxxxx
 
@interact
def _(k=(3,[2..11])):
    F = lambda x: sum([Li(x^(1/j))*moebius(j)/j for j in [1..k]])
    T = [['$i$', r'$\pi(i)$', '$Li(i)$', r'$\pi(i)-Li(i)$', r'$\pi(i)-\sum_{j=1}^{%s} \frac{\mu(j)}{j} Li(x^{1/j})$'%k]]
    for i in [100000,200000..1000000]:
        T.append([i, prime_pi(i), Li(i).n(digits=7), (prime_pi(i)-Li(i)).n(digits=4), (prime_pi(i)-F(i)).n(digits=4)])
    pretty_print(html(table(T,header_row = True, frame = True)))

🔗

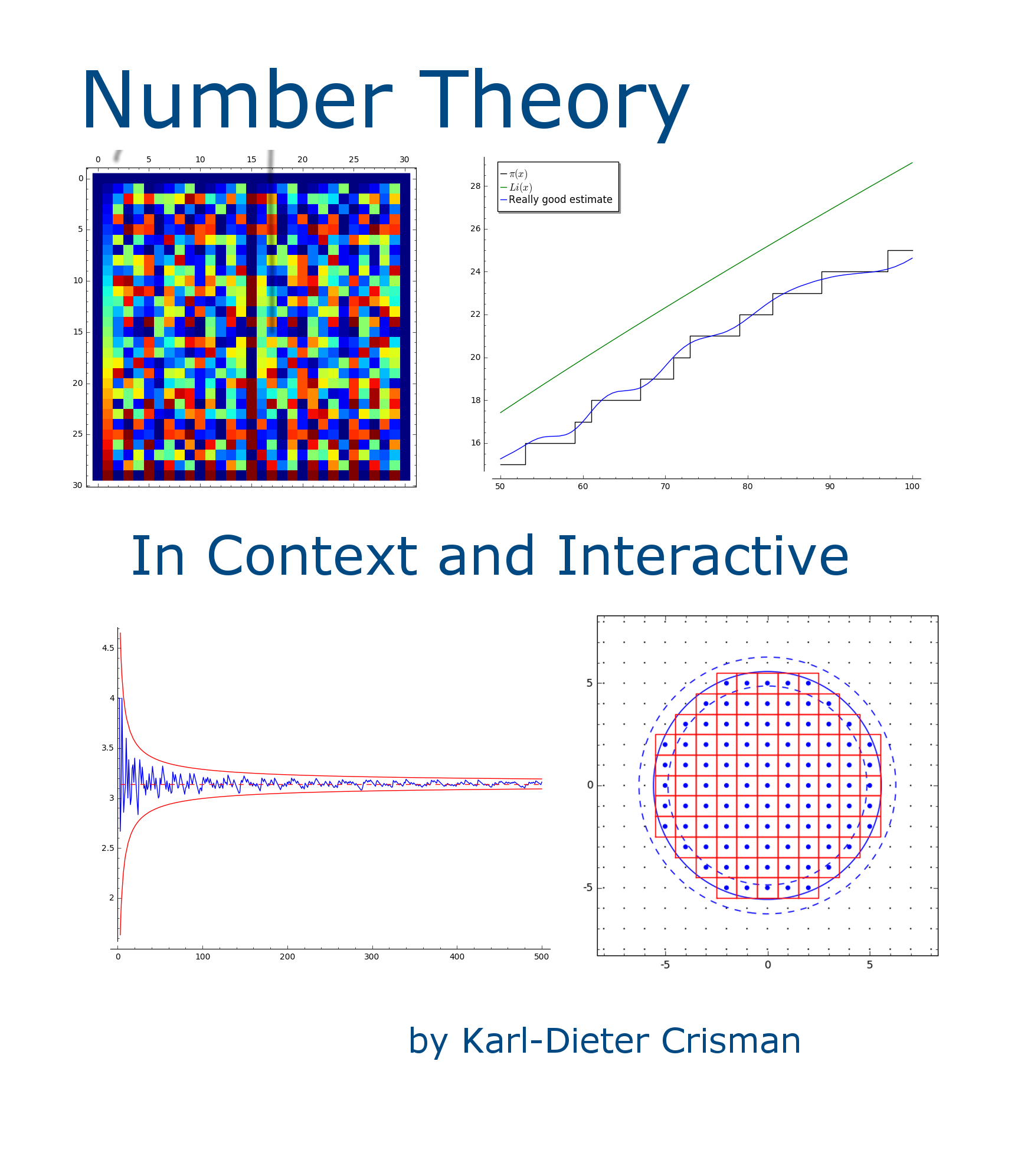
The table shows the errors in Gauss' and our new estimates for every hundred thousand up to a million. Clearly Gauss is not exact, but the other error is not always perfect either.

🔗

After the Prime Number Theorem was proved, mathematicians wanted to get a better handle on the remaining error between the log integral and

$\pi(x)\text{.}$ In particular, the Swedish mathematician Helge Von Koch made a very interesting contribution in 1901.

🔗

Conjecture 25.2.1.

The (absolute value of the) error in the PNT is less than

$\begin{equation*} \frac{1}{8\pi}\sqrt{x}\log(x)\text{.} \end{equation*}$

🔗

This seems to work, broadly speaking. You can try it interactively after the static graphic.

Figure 25.2.2. Von Koch estimate of error in prime number theorem

xxxxxxxxxx
 
@interact
def _(n=(5000,(1000,10^6))):
   P = plot(prime_pi,n-1000,n, color='black', legend_label=r'$\pi(x)$')
   P += plot(Li,n-1000,n, color='green', legend_label='$Li(x)$')
   P += plot(lambda x: Li(x) - 1/(8*pi)*sqrt(x)*log(x),n-1000,n, color='blue',linestyle='--', legend_label="Von Koch error estimate")
   P += plot(lambda x: Li(x) + 1/(8*pi)*sqrt(x)*log(x),n-1000,n, color='blue',linestyle='--')
   show(P)

🔗

Given the observed data, the conjecture seems plausible, if not even open to improvement. Though we should remember that

$Li$ and

$\pi$ switch places infinitely often, see Fact 21.2.5! Of course, a conjecture is not a theorem, but luckily Von Koch had one of those as well.

🔗

Theorem 25.2.3.

The truth of the error estimate

$\begin{equation*} \left|\pi(x)-Li(x)\right|\leq \frac{1}{8\pi}\sqrt{x}\log(x) \end{equation*}$

for the prime number theorem is equivalent to saying that $\zeta(s)$ equals zero precisely where Riemann thought it would be zero in 1859 (see Conjecture 25.3.7).

🔗

This may seem like an odd statement. After all,

$\zeta$ is just about reciprocals of all numbers, and can't directly measure primes. (And what do I mean by “thought it would be”?) But in fact, the original proofs of the PNT also used the

$\zeta$ function in essential ways. So Von Koch was just formalizing the exact estimate it could give us for the error.